The gist for this lambda function can be found here.
You can download an example file here.
The goal
If we have a table of sales of a product where each row represents one month, then we might want to calculate – for each month – the rolling sum of sales over the most recent three months.
When we sum a variable over multiple rows like this, the rows we are summing over are referred to as a “window” on the data. So, functions that apply calculations over a rolling number of rows are referred to as “window functions”.
These window functions are available in almost all flavors of SQL.
They’re also available in the Python pandas package. In pandas, we can use window functions by making calls to rolling.
The goal here is to mimic the functionality seen in pd.rolling by providing a generic and dynamic interface for calculating rolling aggregates over a wide set of functions.
pd.rolling.aggregate – a solution
If you’re not familiar with the concept of a thunk and how it’s used in Excel lambda functions, please read this before continuing.
This is the lambda function pd.rolling.aggregate:
=LAMBDA(x,window,agg,
LET(
_x,x,
_w,window,
_agg,agg,
_aggs,{"average";"count";"counta";"max";"min"
;"product";"stdev.s";"stdev.p";"sum";"var.s"
;"var.p";"median";"mode.sngl";"kurt";"skew"
;"sem"},
_thk,LAMBDA(x,LAMBDA(x)),
_fn_aggs,MAKEARRAY(ROWS(_aggs),1,
LAMBDA(r,c,
CHOOSE(
r,
_thk(LAMBDA(x,AVERAGE(x))),
_thk(LAMBDA(x,COUNT(x))),
_thk(LAMBDA(x,COUNTA(x))),
_thk(LAMBDA(x,MAX(x))),
_thk(LAMBDA(x,MIN(x))),
_thk(LAMBDA(x,PRODUCT(x))),
_thk(LAMBDA(x,STDEV.S(x))),
_thk(LAMBDA(x,STDEV.P(x))),
_thk(LAMBDA(x,SUM(x))),
_thk(LAMBDA(x,VAR.S(x))),
_thk(LAMBDA(x,VAR.P(x))),
_thk(LAMBDA(x,MEDIAN(x))),
_thk(LAMBDA(x,MODE.SNGL(x))),
_thk(LAMBDA(x,KURT(x))),
_thk(LAMBDA(x,SKEW(x))),
_thk(LAMBDA(x,STDEV.S(x)/SQRT(_w)))
)
)
),
_fn,XLOOKUP(_agg,_aggs,_fn_aggs),
_i,SEQUENCE(ROWS(x)),
_s,SCAN(0,_i,
LAMBDA(a,b,
IF(
b<_w,
NA(),
_thk(
MAKEARRAY(_w,1,
LAMBDA(r,c,
INDEX(_x,b-_w+r)
)
)
)
)
)
),
_out,SCAN(0,_i,LAMBDA(a,b,_fn()(INDEX(_s,b,1)()))),
_out
)
)
This is how it works:
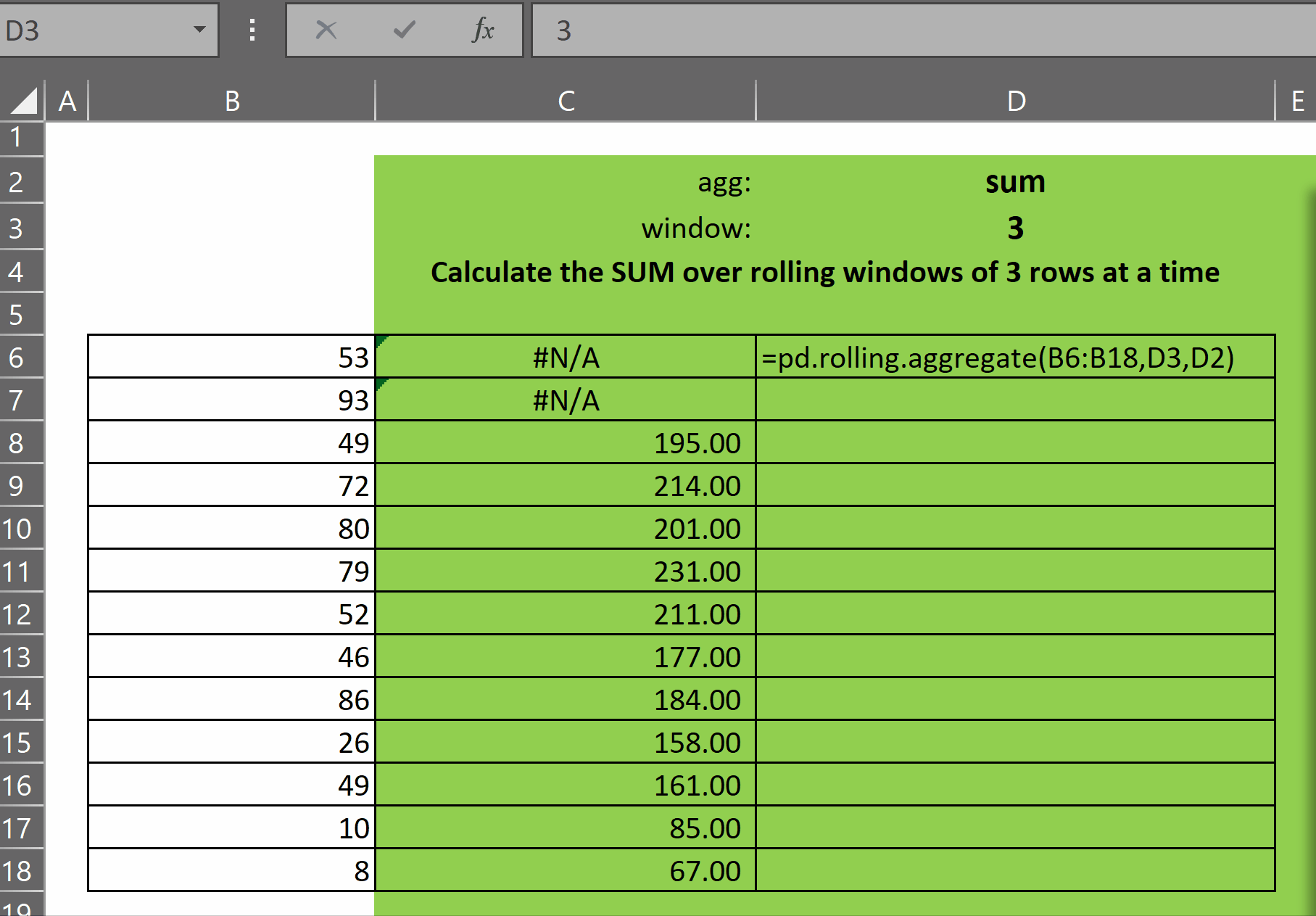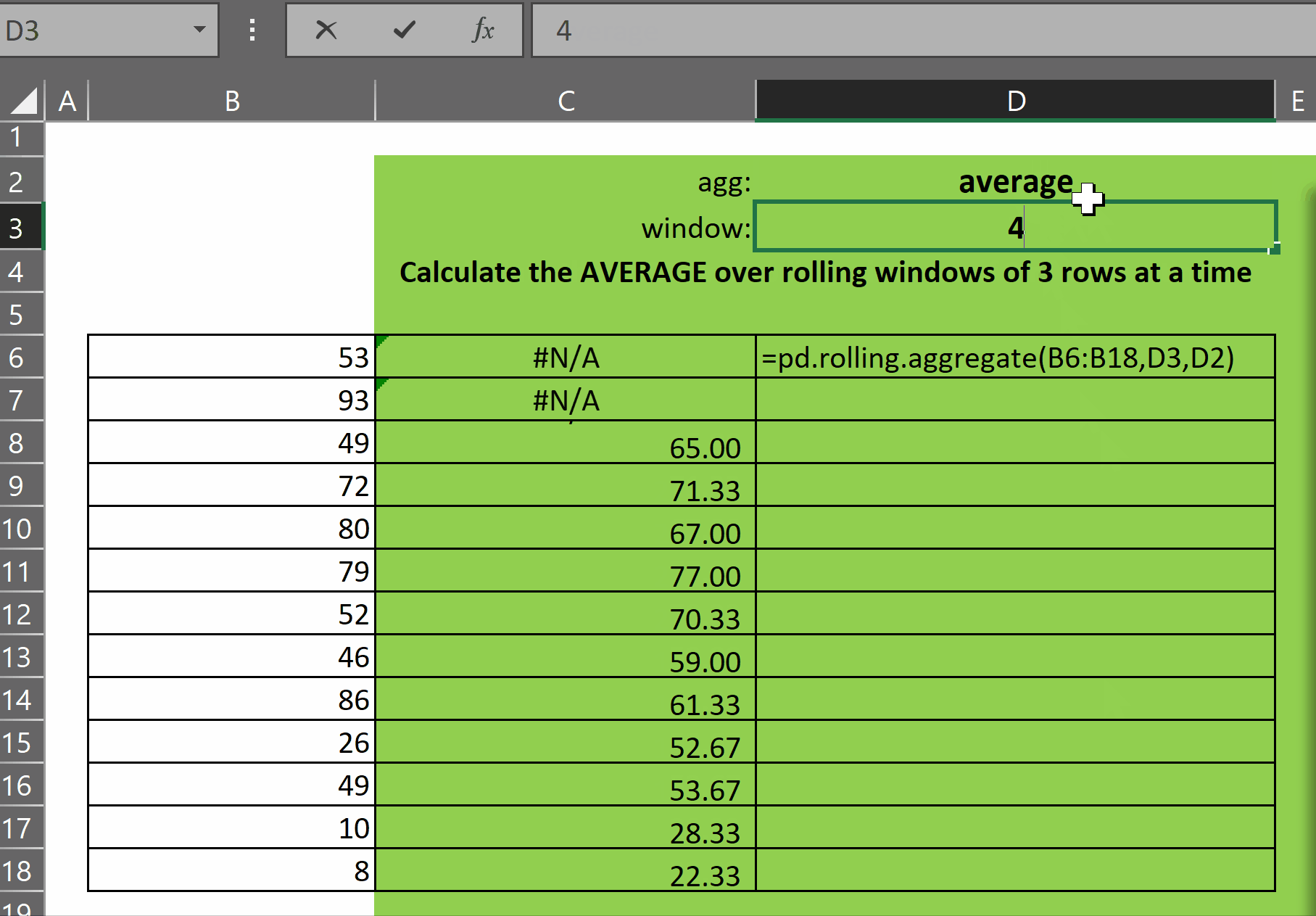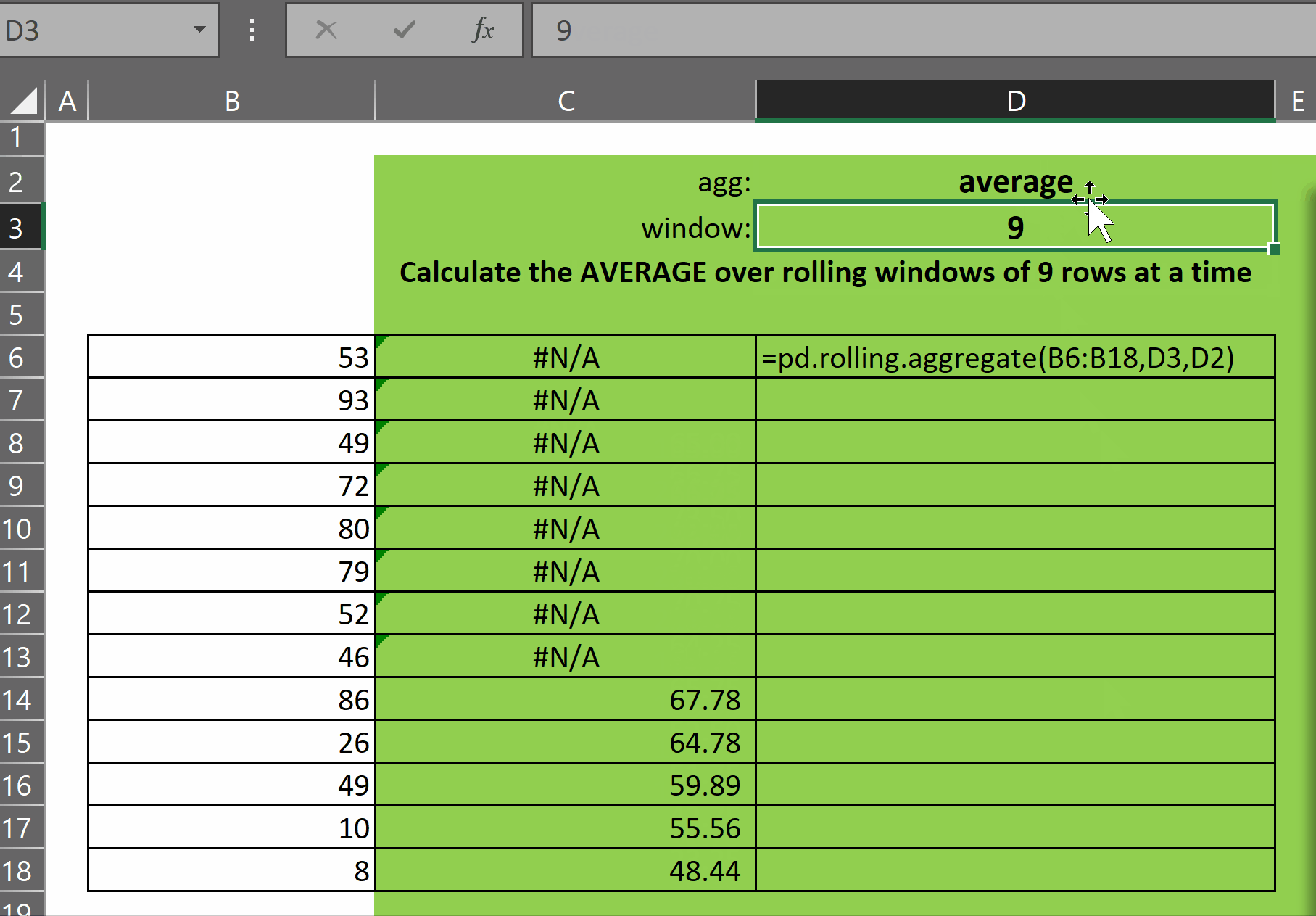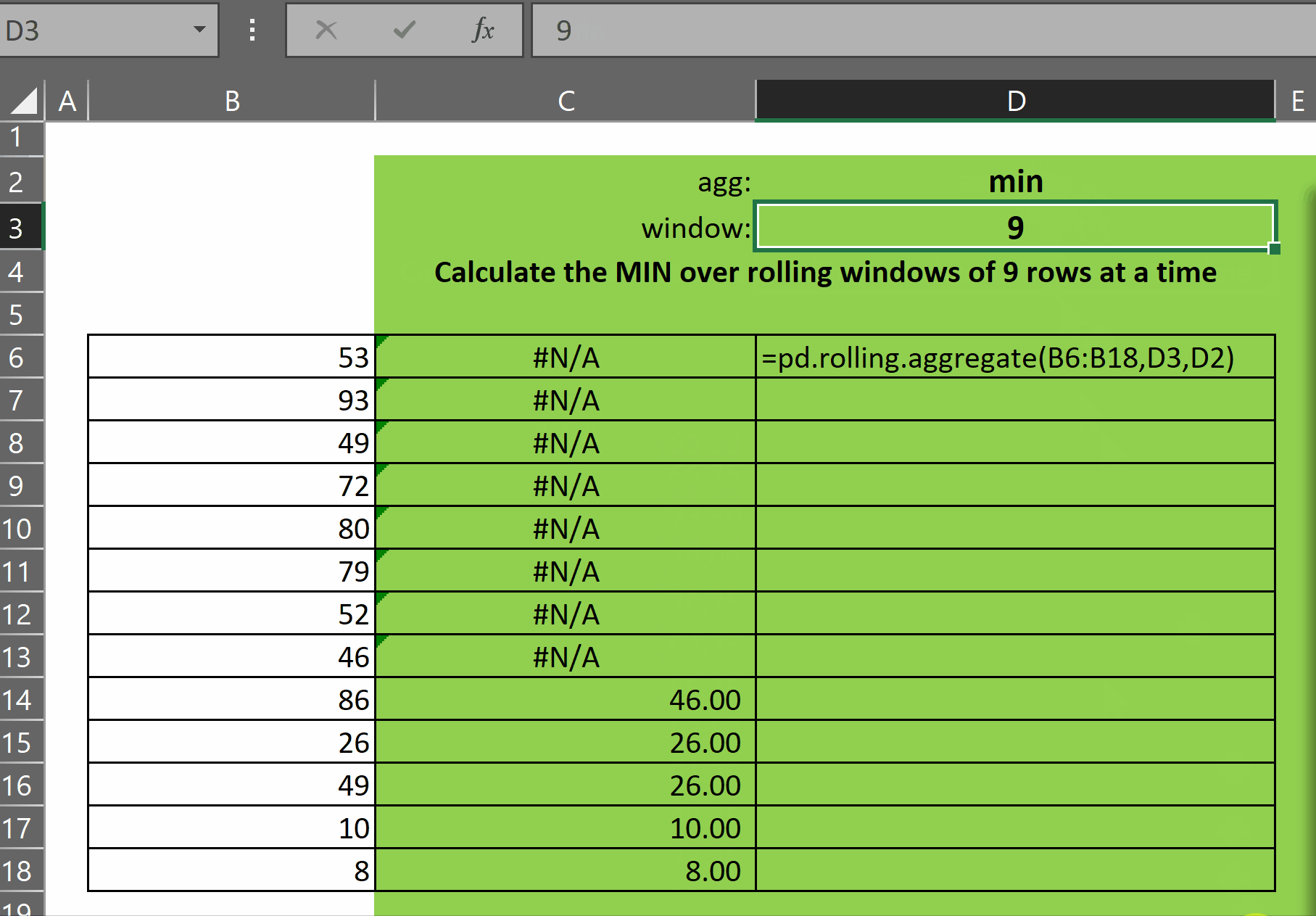
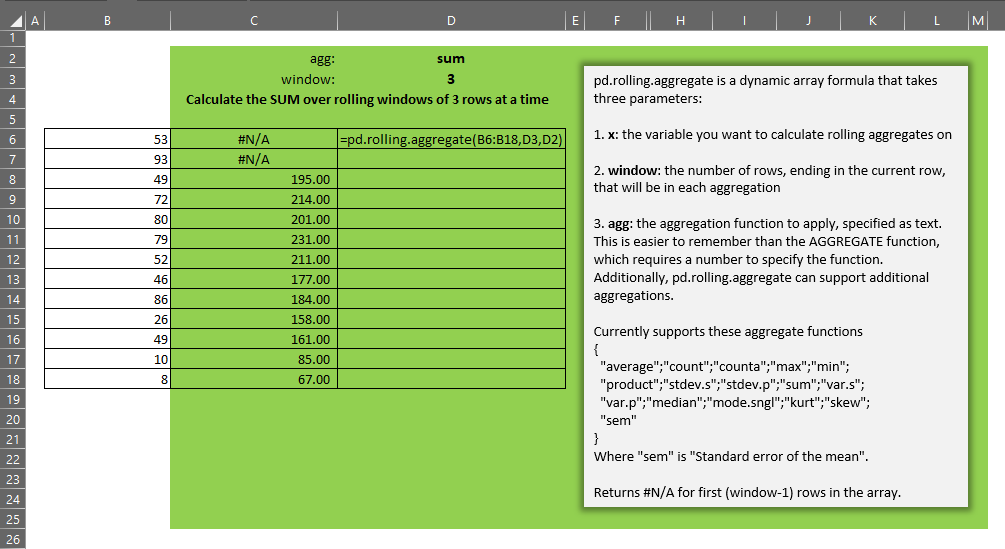
pd.rolling.aggregate takes three parameters:
- x – the single-column array of numbers over which we want to calculate rolling aggregates
- window – an integer representing the size of the window, i.e. the number of most-recent rows ending in the current row, that defines the window for the aggregate that will be displayed on the current row of the output array
- agg – a text representation of the aggregate function we want to apply to each window. You can see in the code above which functions are supported. The good news is that it is incredibly easy to add new customized aggregations to this lambda
As you can see in the gif above, the function returns an array of results of the function agg over each window of size window. The first (window-1) rows display #N/A as there are not enough rows prior to each of those rows to calculate the window function.
pd.rolling.aggregate – how it works
Let’s break it down:
=LAMBDA(x,window,agg,
LET(
_x,x,
_w,window,
_agg,agg,
_aggs,{"average";"count";"counta";"max";"min"
;"product";"stdev.s";"stdev.p";"sum";"var.s"
;"var.p";"median";"mode.sngl";"kurt";"skew"
;"sem"},
We start by defining some variables with LET:
- _x – this is a copy of the parameter x. This is not strictly necessary, but by convention I make a habit of adding a single LET name for each parameter. Sometimes it will include some initialization logic, and sometimes it won’t. In this case, there is no initialization logic
- _w – a copy of the parameter window
- _agg – a copy of the parameter agg
- _aggs – this is a single-column array of supported functions. I’ve taken care to use the exact name of each of the native Excel functions and for the most part they are in the same order as in the native AGGREGATE function. The flexibility that Lambda offers allows us to add as many aggregate functions as we want. In this initial version, I’ve added KURT and SKEW to return the kurtosis and skewness over each window. I’ve also added a calculation for the standard error of the mean, a common statistical measurement. The text for this latter calculation is “sem”
Next we define a thunk for each of the supported aggregate functions. Again, if you’re not familiar with thunks, please read this first.
_thk,LAMBDA(x,LAMBDA(x)),
_fn_aggs,MAKEARRAY(ROWS(_aggs),1,
LAMBDA(r,c,
CHOOSE(
r,
_thk(LAMBDA(x,AVERAGE(x))),
_thk(LAMBDA(x,COUNT(x))),
_thk(LAMBDA(x,COUNTA(x))),
_thk(LAMBDA(x,MAX(x))),
_thk(LAMBDA(x,MIN(x))),
_thk(LAMBDA(x,PRODUCT(x))),
_thk(LAMBDA(x,STDEV.S(x))),
_thk(LAMBDA(x,STDEV.P(x))),
_thk(LAMBDA(x,SUM(x))),
_thk(LAMBDA(x,VAR.S(x))),
_thk(LAMBDA(x,VAR.P(x))),
_thk(LAMBDA(x,MEDIAN(x))),
_thk(LAMBDA(x,MODE.SNGL(x))),
_thk(LAMBDA(x,KURT(x))),
_thk(LAMBDA(x,SKEW(x))),
_thk(LAMBDA(x,STDEV.S(x)/SQRT(_w)))
)
)
),
- _thk – this is a thunk. It’s a lambda with a single parameter of any type. That parameter is stored inside an inner lambda. We can pass any kind of data into a thunk. But importantly – a function or an array can be passed into the thunk.
- _fn_aggs – here we’re using MAKEARRAY to define an array of thunks. Each thunk contains a function that will calculate the aggregation for whatever aggregation we want. By having an array of functions like this, we can use a function like XLOOKUP to retrieve the requested aggregate from the array with minimal hassle
Next up:
_fn,XLOOKUP(_agg,_aggs,_fn_aggs),
_i,SEQUENCE(ROWS(x)),
_s,SCAN(0,_i,
LAMBDA(a,b,
IF(
b<_w,
NA(),
_thk(
MAKEARRAY(_w,1,
LAMBDA(r,c,
INDEX(_x,b-_w+r)
)
)
)
)
)
),
_out,SCAN(0,_i,LAMBDA(a,b,_fn()(INDEX(_s,b,1)()))),
_out
)
)
- _fn – as mentioned above, we use XLOOKUP to retrieve the requested aggregation from the array of thunks using the list of supported aggregations as the lookup array
- _i – here we create a sequence of integers to use as the index which will be scanned through below
- _s – we are using SCAN to iterate through the index _i. For some insight into how SCAN works, you can read this. Here we are iterating through each row of _i. At each iteration, we are comparing the value in the current row – b – (which is an integer between 1 and ROWS(x)) with the value passed as the window parameter – which is the named variable _w. If b is less than _w, then the number of rows in the source data prior to and including the current row is not big enough to support an aggregation of this window, so we place the #N/A value in that row. If b is greater than or equal to _w, then we have enough rows to calculate the aggregate over the window of rows ending in the current row. So, we are using a thunk _thk to store an array of _w rows and one column, containing the rows from b-(window-1) to b in the input array _x. The end result is that _s contains an array of arrays. Each array on each row of _s contains an array with _w rows.
- _out – finally we are scanning once again through _i and using the thunked function _fn (note the empty parenthetical) to apply the aggregate to the array stored in row b of the array of arrays _s. We are able to retrieve the array from that row in the array of arrays _s by activating the thunk with the empty parenthetical (seen after the INDEX function). The result is that each row in _out contains the rolling aggregate agg over each window of size window ending on each row in x
At the very end, LET just returns _out to the spreadsheet.
After finishing this, I realised that it might be useful to either:
- calculate several different window sizes for the same aggregate at once, or
- calculate several different aggregates for the same (or different) window sizes at once
So, next I’d like to show you a wrapper function which uses the function describe above to achieve exactly that.
pd.rolling.aggregates – a solution
This is the wrapper function in question:
=LAMBDA(x,windows,aggs,
LET(
_tr,LAMBDA(arr,LET(x,FILTER(arr,arr<>""),IF(ROWS(x)=1,TRANSPOSE(x),x))),
_a,_tr(aggs),
_w,_tr(windows),
_resize,ROWS(_a)<>ROWS(_w),
_rs,LAMBDA(arr,resize_to,MAKEARRAY(resize_to,1,LAMBDA(r,c,IF(r<=ROWS(arr),INDEX(arr,r,1),INDEX(arr,ROWS(arr),1))))),
_ms,MAX(ROWS(_a),ROWS(_w)),
_ar,IF(_resize,_rs(_a,_ms),_a),
_wr,IF(_resize,_rs(_w,_ms),_w),
_out,
MAKEARRAY(
ROWS(x),
_ms,
LAMBDA(r,c,
INDEX(pd.rolling.aggregate(x,INDEX(_wr,c,1),INDEX(_ar,c,1)),r,1)
)
),
_out
)
)
This is how it works:
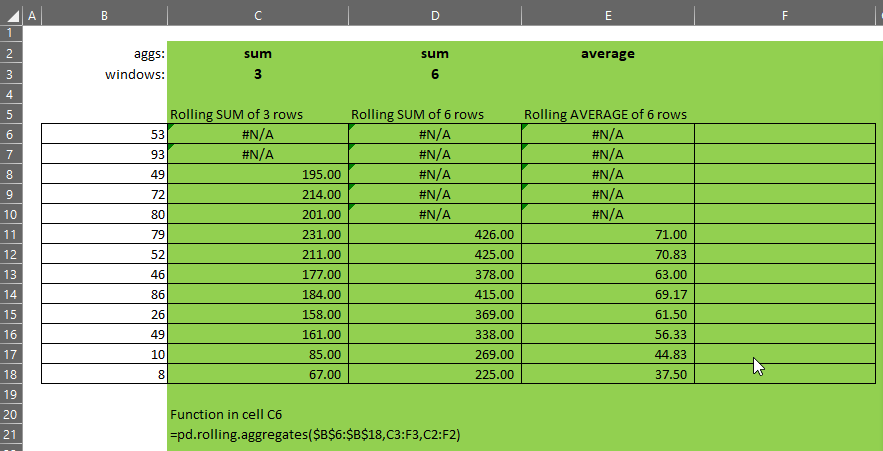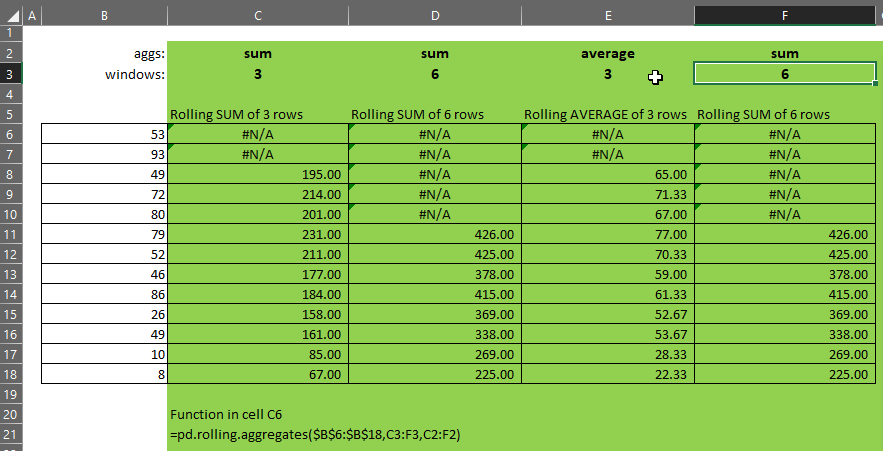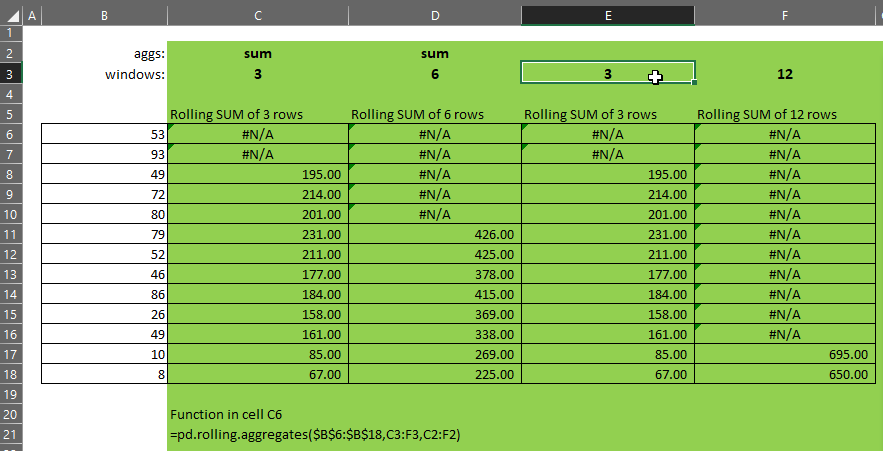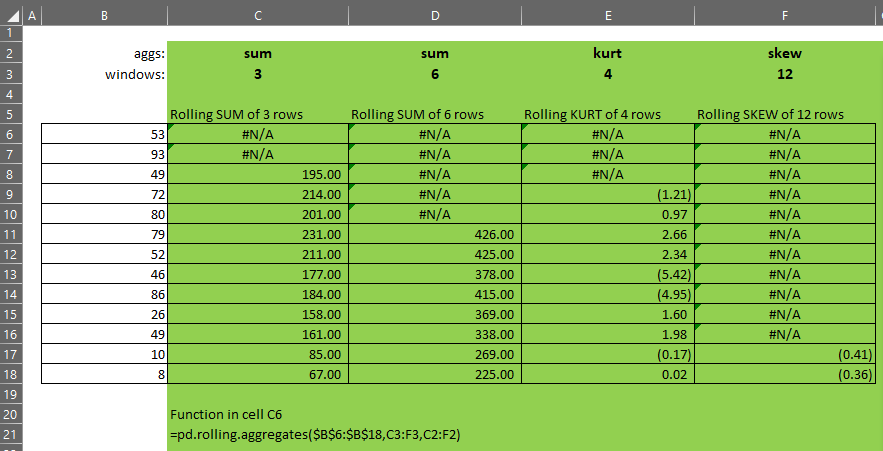
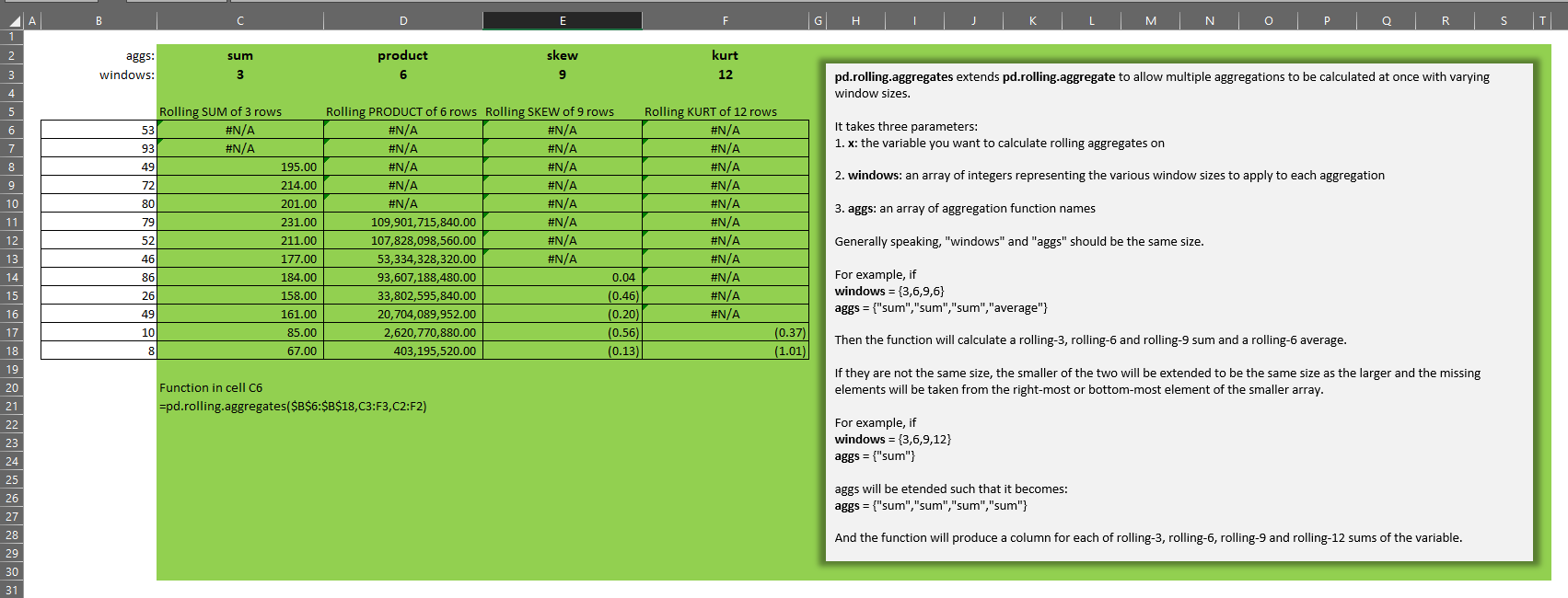
pd.rolling.aggregates takes three parameters:
- x – the single-column array of numbers over which we want to calculate rolling aggregates
- windows – an array of integers representing the size of the windows to be calculated. Each element in this array will be passed as the window parameter to the pd.rolling.aggregate function
- aggs – an array of function names to apply over the windows whose sizes are defined by the corresponding element in the windows parameter
Generally speaking, windows and aggs should be the same size.
- If windows = {3,6,9,6}, and
- aggs = {“sum”,”sum”,”sum”,”average”}, then
- the function will calculate a rolling-3, rolling-6 and rolling-9 sum and a rolling-6 average.
If windows and aggs are not the same size, the smaller of the two will be extended to be the same size as the larger and the missing elements will be taken from the right-most or bottom-most element of the smaller array.
- If windows = {3,6,9,12}, and
- aggs = {“sum”}, then
- aggs will be extended such that it becomes {“sum”,”sum”,”sum”,”sum”}, and
- the function will produce a column for each of rolling-3, rolling-6, rolling-9 and rolling-12 sum.
pd.rolling.aggregates – how it works
=LAMBDA(x,windows,aggs,
LET(
_tr,LAMBDA(arr,LET(x,FILTER(arr,arr<>""),IF(ROWS(x)=1,TRANSPOSE(x),x))),
_a,_tr(aggs),
_w,_tr(windows),
_resize,ROWS(_a)<>ROWS(_w),
_rs,LAMBDA(arr,resize_to,MAKEARRAY(resize_to,1,LAMBDA(r,c,IF(r<=ROWS(arr),INDEX(arr,r,1),INDEX(arr,ROWS(arr),1))))),
_ms,MAX(ROWS(_a),ROWS(_w)),
- _tr – is a lambda function that will act on an array in two ways:
- Remove blanks
- Ensure that the array is a one-column vertical array
- _a – here we apply the function _tr to the input array of aggregation functions aggs
- _w – again, we are using the function _tr to transform the input array of window sizes windows
- _resize – is the boolean (TRUE/FALSE) result of the test of whether _a and _w are the same size
- _rs – is a lambda function that will resize an array to the specified size and when growing the array, fill the new elements with the bottom-most element of the input array. At this point it’s just a function definition and is not actually being used (that comes later)
- _ms – here we find the maximum size of both arrays
Next up:
_ar,IF(_resize,_rs(_a,_ms),_a),
_wr,IF(_resize,_rs(_w,_ms),_w),
_out,
MAKEARRAY(
ROWS(x),
_ms,
LAMBDA(r,c,
INDEX(pd.rolling.aggregate(x,INDEX(_wr,c,1),INDEX(_ar,c,1)),r,1)
)
),
_out
)
)
- _ar – we use the previously calculated _resize boolean to determine whether to apply the _rs lambda to the array _a. In truth, in the case that _resize is TRUE, only one of _a or _w needs to be resized, so there is a little redundancy here, but the impact is minimal
- _wr – similarly, we use the previously calculated _resize boolean to determine whether to apply the _rs lambda to the array _w. Again, in the case that _resize is TRUE, only one of _a or _w needs to be resized. There is a little redundancy here, but the impact is minimal
- _out – finally we are creating an array with ROWS(x) rows and _ms (the largest array size of aggs and windows) columns. The lambda within the MAKEARRAY call is using INDEX to return data from a function call of pd.rolling.aggregate. For each output column c, the pd.rolling.aggregate function is being called with the window size from row c from the array _wr and with the aggregation name from row c of the array of aggregate functions _ar. The effect of this is to return a different {window,agg} to each column of the output array.
Last but not least, the end parameter of LET returns the variable _out to the spreadsheet.
In summary
We have seen how to calculate rolling sum in Excel (and much more).
We walked through the function pd.rolling.aggregate which returns a single-column array of rolling aggregates over a set of windows of parameterized size.
We walked through the function pd.rolling.aggregates, which uses pd.rolling.aggregate to return an array of several sets of rolling aggregations of varying window sizes.
I hope these functions will be of use to you, and if not the functions themselves, then I hope the approach to solving this problem has shown you a few of the ways you can use lambda in Excel to create simple interfaces (functions) for calculations which would otherwise take several steps.
By saving these steps as a lambda function that we trust, we can be sure that they are being applied in the same way every time we use the function.
Let me know in the comments if you have any feedback or questions about this.

Leave a Reply